El nuevo currículo de Matemáticas y las situaciones de aprendizaje
Un problema es mucho más que un ejercicio. Tampoco debería ser una tarea donde simplemente se aplica algo explicado con anterioridad. Se trata de construir conocimiento a través de la resolución de problemas, partiendo de situaciones cercanas -significativas- para el alumnado, y que esto forme parte del día a día de la clase.
Las competencias nos acompañan desde tiempos de la LOE (Ley Orgánica de Educación, 2006), por lo que no son algo nuevo. Sin embargo, los currículos LOMLOE (Ley Orgánica de Modificación de la LOE, 2020) sí que incluyen una importante novedad al definir competencias específicas para cada asignatura, que resultan mucho más ‘operativas’ que las competencias clave. Son útiles para orientar la práctica docente, ya que aterrizan en el saber y hacer propio de cada materia.
En la asignatura de Matemáticas, estas competencias se estructuran en ejes que recuerdan a los procesos planteados originalmente por el National Council of Teachers of Mathematics (NCTM) en sus ‘Principios y estándares’ del año 2000, y que fueron recogidos en el documento de ‘Bases para la elaboración de un currículo’ elaborado por el Comité Español de Matemáticas (CEMat): resolución de problemas, razonamiento y prueba, conexiones, comunicación y representación. En el currículo LOMLOE se añade el socioafectivo como quinto componente, reconociendo la importancia de emociones, actitudes y creencias en el aprendizaje de las matemáticas.
Más que un ejercicio
Podría decirse que, en realidad, todo gira en torno al proceso de resolución de problemas. Y aquí entran en juego diferentes consideraciones, porque la resolución de problemas, como eslogan, es algo muy bonito, sí. Pero, cuando rascamos bajo la superficie, la cosa cambia. ¿Qué es un problema? ¿Es simplemente una tarea donde se aplica algo que me han indicado anteriormente? No, pues un problema es más que un ejercicio.
Si la resolución de problemas es realmente importante, esta no puede quedarse en la periferia de cada tema, reducida a problemas de aplicación, eventualmente interesantes. Debe erigirse en una actividad presente en el día a día, siendo el caldo de cultivo del que emergen los saberes correspondientes a cada etapa. Esto sí que invertiría las clases ‘tradicionales’ (sea lo que sea eso), pasando de una cultura de aula en la que el alumnado recibe una explicación de cómo se hacen las cosas y luego las repite, a una en la que hay actividad matemática para construir conocimiento. Esta actividad se refleja en los ejes competenciales anteriormente mencionados. Más que un método para el aprendizaje se trata de un enfoque. Las matemáticas son una creación cultural e implican modos de pensamiento que superan, con creces, la repetición de procedimientos dados de antemano.
Cuando hablamos de problemas no estamos pensando, necesariamente, en problemas de olimpiada, aunque muchos de ellos puedan tener cabida en diferentes secuencias didácticas. Algo tan aparentemente sencillo como medir una tira de papel con otra que tomaremos como unidad es una situación-problema de pleno derecho. Es más, esta situación ofrece al alumnado una razón de ser para las fracciones, que surgen de la necesidad de comunicar longitudes. Si para medir la tira de tela en cuestión hemos necesitado subdividir la unidad en dos y hemos concatenado cinco de estas subunidades, diremos que la tira mide cinco medios (5/2 u). Además, la tarea es especialmente rica, al aparecer ‘complicaciones’ inesperadas (y bienvenidas), como la discusión acerca de cómo dividir la unidad de medida en tres partes iguales.
Un elemento diferenciador del currículo aragonés LOMLOE son sus orientaciones. Estas tienen un carácter no prescriptivo, pero ayudan a concretar lo máximo posible el significado de competencias, sentidos y saberes. Precisamente, el ejemplo de la medida de tiras aparece entre estas orientaciones.
¿Qué pasa con el contexto?
En didáctica de las matemáticas se habla en términos de situaciones, por lo menos, desde Guy Brousseau y su Teoría de las Situaciones Didácticas. Es decir, desde los años setenta del siglo pasado. Resulta chocante que, últimamente, las redes sociales son un hervidero de propuestas de situaciones de aprendizaje, muchas de ellas con tablas inmanejables donde se cruzan competencias, criterios, saberes y demás organizadores curriculares y que ponen el foco más en la forma que en el contenido. ¿No es, acaso, la situación de las tiras (medir una tira de papel con otra que se toma como unidad) una situación de aprendizaje LOMLOE? Desde luego que sí, no hay más que acudir a la definición de ‘situación de aprendizaje’ en los Reales Decretos de Enseñanzas mínimas.
Quizás, en matemáticas sería preferible hablar de situaciones cercanas y significativas para el alumnado, puesto que hablar de situaciones de la vida cotidiana es confuso. ¿Cotidianas para quién? ¿En qué contexto? ¿Ir de compras? De hecho, ¿tiene que haber un contexto? ¿Qué es un contexto? Intentaremos ilustrar la cuestión a continuación con otro ejemplo, esta vez, de geometría.
En una primera instancia las figuras geométricas se abstraen de formas y cuerpos del mundo real. Por eso, en los primeros niveles de razonamiento podemos decir que un rectángulo es como una puerta o que un cuadrado es como una ventana. Sin embargo, conforme progresamos en los niveles de razonamiento y queremos pasar a trabajar clasificaciones de cuadriláteros, lo haremos con entidades abstractas, no con puertas o ventanas. Las actividades de clasificación de cuadriláteros y otras figuras con criterios exclusivos, primero, e inclusivos, después, bien planteadas, son situaciones de aprendizaje en toda regla. En ellas se explora, se toman decisiones, se argumenta y, después de todo eso, se organizan los resultados de aprendizaje.
El término ‘contexto’ en matemáticas no implica algo real necesariamente. Y la palabra ‘cercano’ no implica algo de la vida cotidiana, sino algo que sea significativo. Evidentemente, habrá un problema cuando introducimos capas de abstracción innecesarias, pero eso es otra historia.
Van Den Heuvel-Panhuizen, una de las autoras más representativas de la Enseñanza Matemática Realista señala que "el mundo de la fantasía o de los cuentos de hadas e incluso el mundo formal de las matemáticas [como los cuadriláteros que mencionábamos en el ejemplo anterior] pueden proporcionar contextos adecuados para un problema, siempre que sean reales en las mentes de los alumnos y puedan experimentarlos como tales".
Construir matemáticas implica partir de los conocimientos previos del alumnado, proporcionando experiencias de aprendizaje que los hagan aflorar y que conecten con los saberes que emergen en la resolución de una situación de aprendizaje.
Introducir el teorema de Pitágoras
No se trata de reinventar la rueda. Simplemente, hemos de tener en cuenta que, desde los años ochenta del siglo pasado, se ha trabajado mucho en la línea de las situaciones de aprendizaje. Se trata de tener presente que los mejores ejemplos de ‘repositorios’ de actividades (situaciones de aprendizaje) son aquellos que, o están realizados por un equipo altamente especializado y coordinado, o surgen en el marco de un programa de desarrollo profesional serio. Ejemplo de esto son los materiales de NRICH, de la Universidad de Cambridge, o del Shell Center for Mathematical Education. Por cierto, gran parte de las actividades de NRICH tienen un contexto intramatemático y pocos se atreverían a defender que no por ello no son excelentes situaciones de aprendizaje.
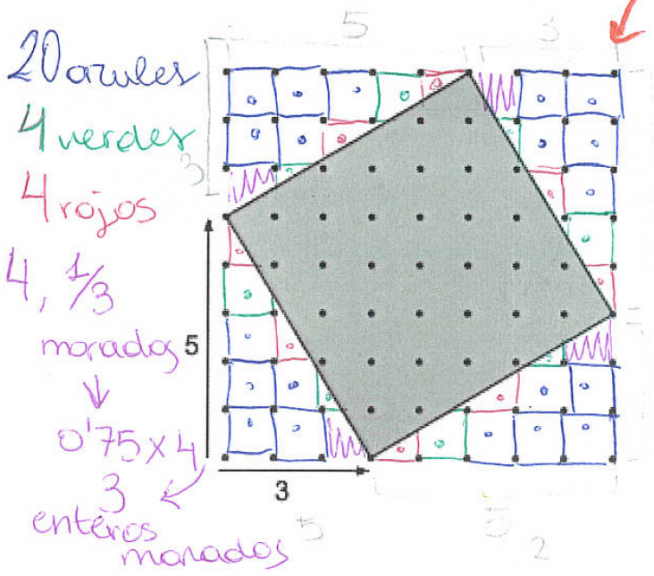
Encontramos una secuencia para introducir el teorema de Pitágoras a través de la resolución de problemas, inspirada en estos materiales, en este artículo. Ahí se parte del problema de calcula el área de un cuadrado ‘inclinado’ en un geoplano. Claro, si no sabes el teorema en cuestión, tienes que apañarte con el cálculo de áreas de manera directa. De esta forma, conectamos con los conocimientos previos del alumnado. A partir de aquí la secuencia continúa generalizando una sucesión de cuadrados de este tipo hasta llegar al archiconocido resultado, dotándolo de significado en una secuencia inclusiva de suelo bajo y techo alto, pues se llegan a relacionar diversas justificaciones del teorema.
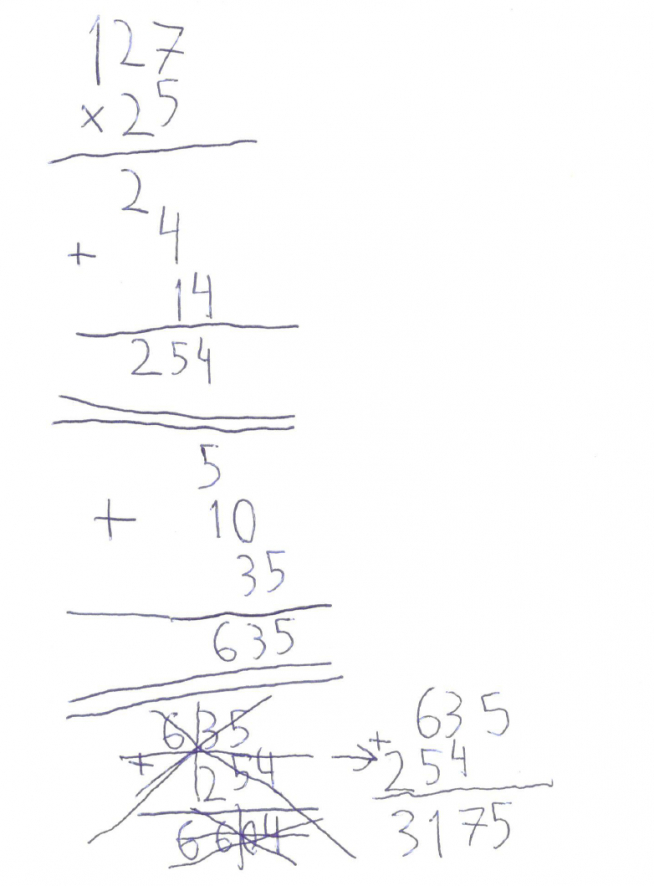
Situaciones de aprendizaje para conectar
Una situación de aprendizaje no tiene por qué ir siempre orientada a la construcción de conocimiento claramente nuevo para el alumnado, como el ejemplo de la de las tiras de fracciones o el de Pitágoras. Supongamos que, atendiendo al currículo, hemos trabajado el algoritmo de la multiplicación para desarrollar el pensamiento computacional y profundizar en el sistema de numeración posicional. Habremos realizado esto con manipulativos y mucha interacción en grupos pequeños de tres alumnos en el aula. Después de ello, queremos continuar. No lo haremos con hojas y hojas de multiplicaciones, sino con actividades de práctica rica que exijan dotar de sentido a lo que se hace. Por ejemplo, ¿qué pasaría si empezamos a multiplicar de izquierda a derecha? En la figura que aparece al lado, tenemos una producción donde, además, se observa el papel que juega el error en el proceso de aprendizaje y al que hay que dotar de valor.